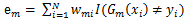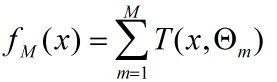分类 决策树 下的文章

决策树学习采用的是自顶向下的递归方法，其基本思想是以信息熵为度量构造一颗熵值下降最快的树，到叶子节点处，熵值为0。其具有可读性、分类速度快的优点，是一种有监督学习。最早提及决策树思想的是Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法，以及Breiman等人在1984年提出的CART算法。决策树的构造过程一般分为3个部分，分[...]

决策树的优点是简单，逻辑清晰，具备可解释性，但是也有一个很大的缺点：非常容易过拟合，解决过拟合的方法主要是有剪枝、随机森林等。从随机森林的名字上就能猜出，这种方法无非是信奉”人多力量大“这句话，把诸多决策树集成在一起，进而形成一个更强大的树树树模型。随机森林是一个Bagging方法，Bagging是一种有放回抽样方法：取出一个样本加入训练集，然后再[...]

Boosting 是一类算法的总称，这类算法的特点是通过训练若干弱分类器，然后将弱分类器组合成强分类器进行分类。为什么要这样做呢？因为弱分类器训练起来很容易，将弱分类器集成起来，往往可以得到很好的效果。俗话说，"三个臭皮匠，顶个诸葛亮"，就是这个道理。这类 Boosting 算法的特点是各个弱分类器之间是串行训练的，当前弱分类器的训练依赖于上一轮弱[...]

提升树模型采用加法模型（基函数的线性组合）与前向分步算法，同时基函数采用决策树算法（对待分类问题采用二叉分类树，对于回归问题采用二叉回归树）。提升树模型可以看作是决策树的加法模型： 其中T()表示决策树，M为树的个数， Θ表示决策树的参数。提升树算法采用前向分部算法，首先确定f0(x) = 0，第m步的模型是：对决策树的参数Θ的确定采用经验风险最小[...]

掌握决策树，我们需要学会如何划分一个决策树， 也有明白修枝的策略，这也是构建决策树很重要的部分。一、决策树为什么要修枝修枝主要解决决策树学习算法中的过拟合问题。比如说，我们要给身高180cm，体重75kg的小明做一件裤子。一般情况下，只要根据小明的身高， 体重， 腰围这三个参数， 就可以做出来一件适合小明穿的裤子，这种裤子和小明同体型的人都可以匹配[...]