分类 决策树 下的文章

集成学习大致可分为两大类：Bagging和Boosting。Bagging一般使用强学习器，其个体学习器之间不存在强依赖关系，容易并行。Boosting则使用弱分类器，其个体学习器之间存在强依赖关系，是一种序列化方法。Bagging主要关注降低方差，而Boosting主要关注降低偏差。Boosting是一族算法，其主要目标为将弱学习器“提升”为强学[...]

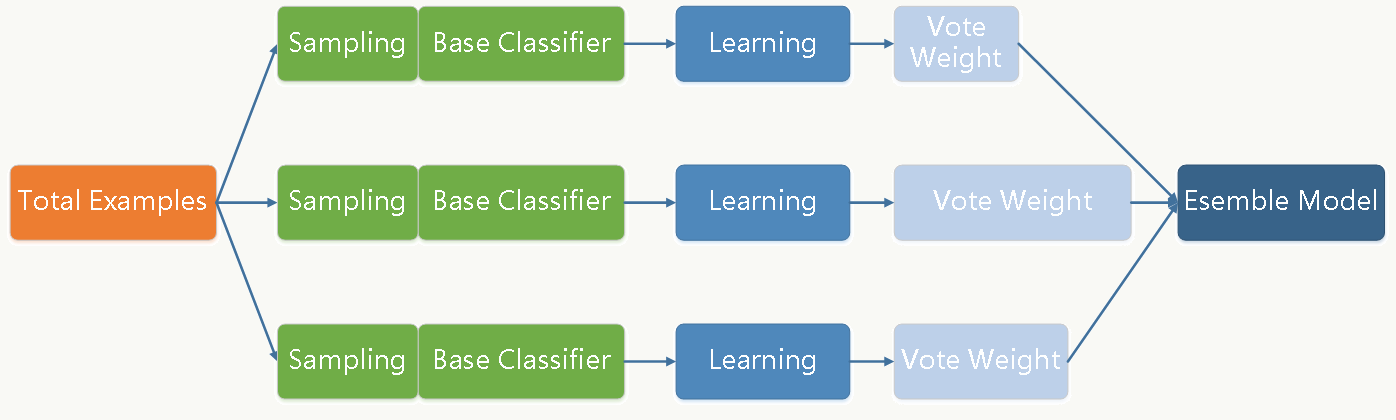
Bagging和Boosting是两类最常用的模型融合解决方案。Bagging方法是通过对训练样本和特征做有放回的抽样，并拟合若干个基础模型，进而通过投票方式做最终分类决策的框架。每个基础分类器（可以是树形结构、神经网络等任何分类模型）的特点是低偏差、高方差，框架通过加权投票方式降低方差，使得整体趋于低偏差、低方差。 其示意图如下所示： Boost[...]

基尼不纯度越小，纯度越高，集合的有序程度越高，分类的效果越好。基尼不纯度为 0 时，表示集合类别一致。基尼不纯度的大概意思是，一个随机事件变成它的对立事件的概率。例如，一个随机事件X ：P(X=0) = 0.5，P(X=1)=0.5那么基尼不纯度就为：P(X=0)(1 - P(X=0)) + P(X=1)(1 - P(X=1)) = 0.5一个随机[...]

C4.5算法是由Ross Quinlan开发的用于产生决策树的算法。该算法是对Ross Quinlan之前开发的ID3算法的一个扩展。C4.5决策树是ID3决策树的改进算法，它解决了ID3决策树无法处理连续型数据的问题以及ID3决策树在使用信息增益划分数据集的时候倾向于选择属性分支更多的属性的问题。它的大部分流程和ID3决策树是相同的或者相似的。 [...]

信息增益比（GainRatio）的定义：在选择决策树中某个结点上的分支属性时，假设该结点上的数据集为DataSet，其中包含Feature个描述属性，样本总数为len(DataSet)或者DataSet.shape[0]，设描述属性feature(不同于Feature，Feature是属性的个数，取值为DataSet.shape[1]，featur[...]